|
运动物体质量随速度而变化的相对性效应是一种客观存在的事实,这个现象在爱因斯坦相对论发表之前,就已被发现,那么,在把物体惯性质量看作速度的函数的情况下,用牛顿定律是否也能推出运动物体的相对性效应来呢?如果这条道路能走得通的话,那么,对物理学的发展将有重大意义。这首先要涉及到对牛顿第二定律本质的重新认识。
在经典力学中,物体运动速度同光速相比一般是很小的,因此,物体的质量在运动过程中,即使考虑相对性效应,质量变化也是极微小的,这在牛顿力学创立的时代,依据当时的实验条件和人们的日常观测,是根本不可能发现的。人们通常将物体质量m当作常量来处理。在这种情况下,静止质量为m0,以速度V ( V << C )运动的物体,其动能表达式为:
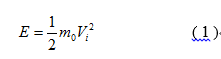
这样近似处理在宏观物体低速运动的范围内是完全适用的,并且具有足够的精确性。
此公式的近似性并不是一开始就为人们所了解的,从1687年牛顿发表力学定律直到二十世纪初的二百多年里,人们一直是把它看作是绝对可靠的。1901年德国人考夫曼通过荷质比测量首先发现了阴极射线的质量随速度而增加的相对性效应,他在题为《贝克勒尔射线的磁偏转性和电偏转性以及电子的视在质量》的论文中写道:“在观测到的速率范围内,e/m有剧烈的变化,随着v的增加,e/m比值下降得非常明显。由此可见,的确有并非微不足道的‘视在质量’,它以这样的方式随速度增加:当达到光速时,它将变为无穷大”。① 1905年,爱因斯坦提出狭义相对论解释了相对性效应。根据相对论,物体质量同其运动速度之间存在如下关系:
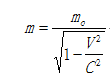
这里m0是相对参照系静止时物体的质量,m是物体相对参照系以速度V运动时的质量。正是运动物体质量随速度变化的相对性效应的发现,人们才开始认识到把运动物体质量看作常量给计算结果所带来的近似性。从质速关系式知道,一个相对于参照系静止的物体,只要物体运动状态一改变,物体的质量就不是m0了,所以,只有当V0→0时,才有m→ m0;同时,只有当 △V→0,才有 △m→0,在这种情况下,我们才能把m看作常量,用m0代替。这就是说,只有在物体运动同时满足V0→0, △V→0时,物体动能表达式才是正确的。可以看出,满足这些条件的点只是在一个包括V0 = 0在内的极小区域内。
那么,当物体具有任意速度Vi以及与此对应的质量mi时,物体的动能将如何求得呢?

我们可以把物体从V0增加到Vt的过程分成n个区间,那么,对于每一个Vi ,物体质量为mi ,我们只要使每一个区间分得足够小,在区间内都能满足mii→ mi-1 ,Vi →Vi-1 ,这样,我们在每一个子区间内,都可以把物体的运动当作是以mi为常量的匀加速运动来处理。然后求出各子区间外力Fi所作的功Wi ,将n个子区间的功全部加起来,就可以得到物体从V0变化到Vt的动能增量。见( 图 1)
在求任意状态物体动能时,必须要将牛顿第二定律作合理推广,即把其中的惯性质量m理解成可变化的。这要从自然界本身存在的质量随速度变化的相对性效应,去反思牛顿第二定律的原来含义中去追寻原因。在F= m a 中,牛顿第二定律本身只是描述一个瞬间过程,即物体在受到外力作用瞬间产生加速度的变化状态。而物体运动状态的完成是有个过程的,表现在物体运动速度变化的完成。从初始速度V0变成另一状态速度Vt,这时物体增加的动能就代表着力的作用过程完成。牛顿在《自然哲学的数学原理》中是这样来叙述第二定律的:“运动的变化永远跟所加的外力成正比,而且是沿着外力作用的直线方向发生的”,“如果一个力产生一个运动,则两倍大的力产生两倍大的运动。无论这力是同时施加的,或逐渐和持续施加的”。②所以,牛顿第二定律里的全部物理量都应该是瞬间量。F是指加在物体上的瞬间作用力,a是指产生的瞬间加速度,m就应该是物体受力瞬间该物体所具有的惯性质量。由于这个质量是随速度变化的,那么,受力瞬间的物体惯性质量则由该物体所处的运动状态决定,即由物体所具有的运动速度Vi来确定。即Fi=mi ai
这样的推广并没有改变牛顿第二定律的内容,而恰恰是恢复牛顿第二定律的真实本质。长期来,人们之所以把m当作常量对待,乃是受当时物理学发展水平的限制,那时,人们还没有发现运动物体质量的相对性效应,因为,在当时的实验条件下,无法测量出在物体低速运动时所引起的质量的微小变化。所以,人们一直认为,物体的质量m在运动状态变化过程中是不变的。以后,人们就自然而然的把m当作常量延用下来了。如果当时在考夫曼的实验基础上,人们能及时对牛顿定律进行改造的话,那么,也许可能会在另一条与狭义相对论不同前提的道路上推出某些同狭义相对论相似的结论来。
现在,我们利用牛顿第二定律Fi=mi ai 来求具有任意速度V运动物体的动能。对于(图1)的n个间隔中的每一个子区间,只要分得足够小,我们都可以用匀加速运动来处理。

这就是要证明的结论。这一公式不仅适用于低速运动的物体,同样也适用于高速运动的物体。
物体动能表达式从(1)式变化成(2)式,这一改变有着重大的理论意义。首先,对于(2)式来讲,虽然是在经典力学的基础上推导出来的,同牛顿力学里的动能表达式(1)形式上完全一样,但是,它已经具有了相对论性的特点,它是在物体质量同速度变化有关的事实已被发现的基础上,对牛顿定律进行重新审查后所作出的一种合理的推广。这种推广将使牛顿定律能适合于物体以任何速度运动的情况。
但是,同相对论本身存在的问题一样,这种推广仍然没有揭示出造成运动物体质量相对性效应的原因和机制,而仅仅是更合理地在运用牛顿定律描述物体的运动规律。
我们在牛顿力学的框架里,不可能找到造成运动物体质量随速度变化相对性效应的原因,同样,爱因斯坦相对论虽然得出了相对性效应的质速关系式,但仍然没有找到造成相对性效应的本质原因。矛盾的焦点又归结到了一些至今也没解决的物理学基本哲学问题:“力”的本质是什么?“力”的作用过程是否存在物质的转移?能量是否必须有荷载粒子?能量和物质可以分离吗?如果把“力”的作用过程看作是物质的转移过程,那么运动的物体质量发生变化就是必然的。这恰恰是坚持了唯物主义。
值得注意的是:牛顿万有引力定律与爱因斯坦的质速关系式之间隐含着矛盾,根据质速关系,运动速度越大,物体的质量就越大;按万有引力定律,质量越大引力就越大,物体应被地球引力拉得更紧。但是,事实恰恰相反,随着物体运动速度增加,物体争脱地球引力的能力也增加。物体运动状态改变时所显示出来的两种矛盾的特征(速度增大,质量增加,万有引力却减少;速度减少,质量减少,万有引力却增加),预示着物体运动状态变化的某种内在原因:它仿佛是由于运动物体吸收了一种具有同引力相反性质的物质粒子。这是一种具有对抗引力特性的能量粒子——斥力子,作为实物粒子,它当然应该具有质量、能量、动量,它在作用物体之间的转移,就构成了物理学中各种质量、能量、动量守恒定律。因此,物理学需要寻找一种新的物质作用粒子,只有把具有对抗引力的作用粒子引入物理学,才能使相对论同牛顿力学、量子论融合起来。
(本文引自《相对论再思考》 北京 地震出版社2002年 p84-p87;)
参考文献:
① W.Kaufmann,Gottinger Nachrichten,Nov.8,1901. 转引自申先甲等:《物理学史简编》山东教育出版社1985年 629
② I.牛顿:《自然哲学的数学原理》 1803年版 转引自W.F.马吉:《物理学原著选读》 商务印书馆北京 1986年42
③申先甲等:《物理学史简编》山东教育出版社1985年 627-628
(责任编辑:admin) |
